The Answer Report contains the original guess for the solution and the final value of thesolution as well as the objective function values for the original guess and final value.
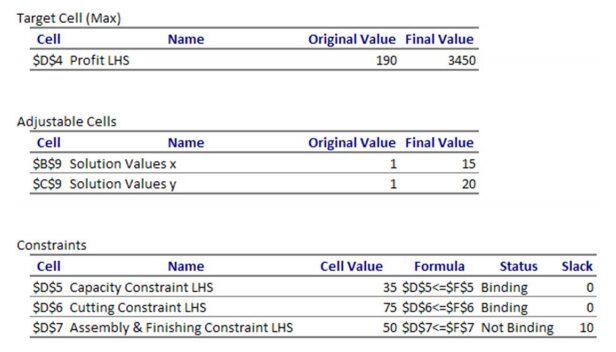
The report also indicates that the capacity and cutting constraints are binding, so all of the capacity and cutting time is utilized in the final solution. The assembly and finishing constraint is not binding with 10 hours of slack. This means there is 10 hours of assembly and finish time that is not being used to produce the final solution.
The Sensitivity Report details how changes in the coefficients of the objective function affect the solution and how changes in the constants on the right hand side of the constraints affect the solution. Under the heading “Adjustable Cells”, the three columns labeled “Objective Coefficient”, “Allowable Increase”, and “Allowable Decrease” give us the conditions for which the solution (15, 20) remains optimal.
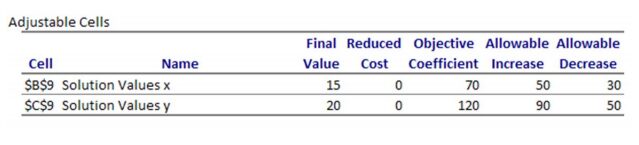
For instance, if the coefficient on x is raised to 70 + 50 = 120 , or decreased to 70 − 30 = 40 40, the optimal production plan is to produce 15 frame bags and 20 panniers. Similarly, if the coefficient on y is raised to 120 + 90 = 210 , or decreased to 120 − 50 = 70 , the optimal production plan remains unchanged.
In each case, we can calculate the range of values that the coefficient can take on by subtracting the allowable decrease from the coefficient or adding the allowable increase to the coefficient.
In terms of the application, this means that if the profit per frame bag varies between 40 and 120 or the profit per pannier varies between 70 and 210, the optimal production plan is to produce 15 frame bags and 20 panniers per week. These values match the values we discovered earlier in the section using the graph of the feasible region.
The second part of the Sensitivity Report examines how changes to the right hand side of any constraint affects the optimal solution. A change to the constant on the right hand side of a constraint changes the size of the feasible region. Increasing the right hand side of any constraint with positive coefficients shifts the border matching the constraint up. Decreasing the right hand side of any constraint with positive coefficients shifts the border matching the constraints down. The shadow price indicates how the objective function will change when the constant on the right hand side is changed.
In the table, the shadow price for the capacity constraint is 45. This indicates that if the capacity is increased by 1 (from 35 to 36), the corresponding profit at the optimal solution will increase by $45. Similarly, if the capacity is decreased by 1 (from 35 to 34), the profit at the optimal solution will decrease by $45. In both cases, since the size of the feasible region changes, the optimal solution changes to a new value.
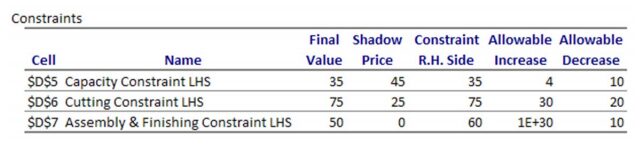
These changes are valid over a range of changes indicated by the values in the “Allowable Increase” and “Allowable Decrease” columns. As long as the right hand side stays within 35 −10 = 25 to 35 + 4 = 39 , the shadow price is valid.
The same reasoning applies to the other binding constraint in the linear programming problem. If the amount of time for cutting increases/ decreases by 1 hour in a range of values from 75 − 20 = 55 hours to 75 + 30 = 105 hours, the profit will increase/decrease by $25.
The sensitivity analysis for a nonbinding constraint, like the assembly and finishing constraint, is different. At the optimal solution, changes to the right hand side do not affect the profit as long as the right hand side is not decreased too much. This means that the shadow price is $0. The only way this would change is if the number of hours for assembly and finishing is dropped to 50 hours. At this point, there is no longer any slack at the optimal solution and the constraint becomes binding.
This fact is evident in the report under the “Allowable Decrease” column.
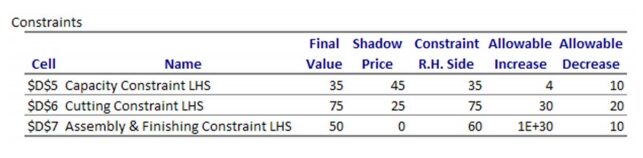
For the assembly and finishing constraint, the shadow price of $0 is applicable for a decrease of 10 hours from 60 hours or 50 hours. The “Allowable Increase” for this constraint is show as 1E+30. This is Excel’s way of showing infinity. This means that the right hand side can be increased any amount without changing the shadow price. This should make sense since increasing the right hand side (adding more hours for assembly and finishing) simply adds more unutilized time to the constraint and will not change the feasible region. As expected, Excel’s Sensitivity Report mirrors the conclusions we drew from analyzing the constants in the constraints graphically.
Excel can also be used to find and analyze the solution to a standard minimization problem.
Example 1. Analyze the Sensitivity Report for a Standard Minimization Problem
In Sections 4.2 and 4.4, we solved the minimization problem

where C is the cost of contracting Q1 barrels of American ale from contract brewery 1 and Q2 barrels of America ale from contract brewery 2.
Use Excel to solve and analyze the associated standard minimization problem

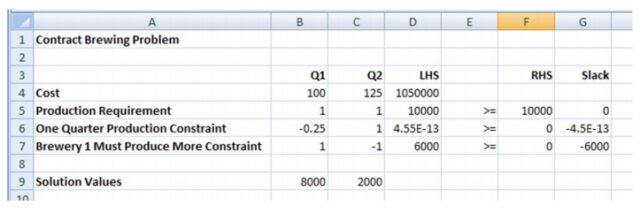
Solution. Follow the steps earlier (with appropriate modifications) to create the worksheet below.
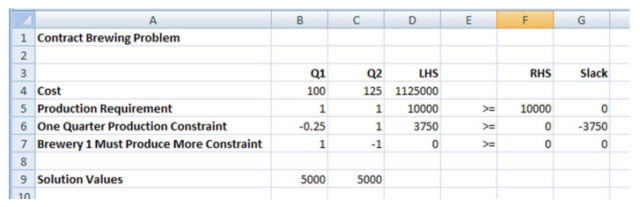
Be careful to use the SUMPRODUCT function correctly in cells D4 through D7.
The Solver Parameters are as follows:
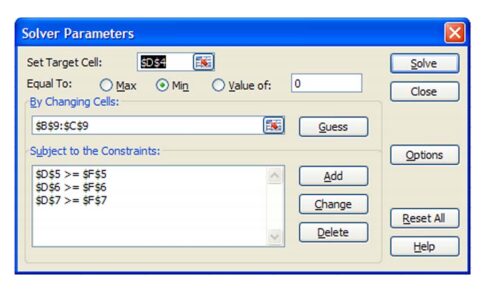
Also make sure you set the Solver Options properly. If you do not set the options properly, the Sensitivity Report will not look like the one presented earlier.
The worksheet below shows the final solution.
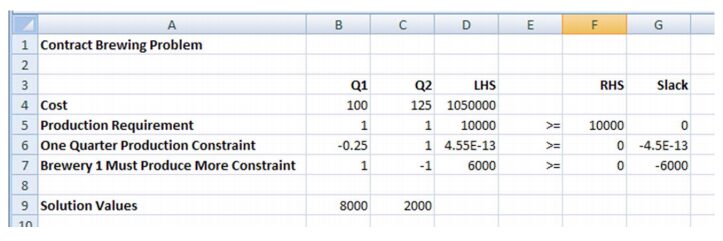
According to the worksheet, 8000 barrels should be contracted from brewery 1 and 2000 barrels from brewery 2. This results in a minimum cost of $1,050,000. Notice that the slack in the second constraint is -4.5E-13. This is approximately zero and nothing to be concerned about.
By examining the objective coefficients, we can determine the range of values over which (Q1,Q2 ) = (8000, 2000) remains optimal.

If the cost per barrel at brewery 1 is as high as 100 + 25 = 125 dollars or as low as 100 −131.25 = −31.25 dollars and we hold the cost per barrel at brewery 2 at $125, this solution remains optimal. The cost per barrel cannot be negative so realistically the cost per barrel can be between $0 and $125.
If the cost per barrel at brewery 2 is greater than 125 − 25 = 100 dollars and the cost per barrel is held constant at $100, the solution is still optimal. The number 1E+30 under allowable increase indicates the coefficient can be increased without bound.
Now let’s look at the other table in the Sensitivity Report.

The first constraint requires that the breweries supply at least 10,000 barrels and is binding. The shadow price of $105 is valid for a production requirement as low as 10, 000 −10, 000 = 0 and infinitely high. The shadow price of $105 indicates that if the production requirement is increased by one barrel within this range, the cost will increase by $105.

The shadow price for the second constraint indicates how the cost will change if the right hand side of −0.25Q1 + Q2 ≥ 0 is increased by one barrel. Since this inequality is equivalent to Q2 ≥ 0 + 0.25Q1 , increasing the constant by 1 unit is the same as changing the requirement that the number of barrels from brewery 2 be at least one quarter the number of barrels from brewery 1 to a requirement that the number of barrels from brewery 2 must be at least one more than one quarter of the number of barrels from brewery 1. With this change in the requirement, the cost will increase by $20. This cost increase is valid for constants on the right side from -2500 to 3750.
The third constraint is not binding. As long as the constant on the right hand side of Q1 − Q2 ≥ 0 is less than 6000, changing the constant by one barrel does not change the cost.












